
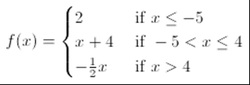
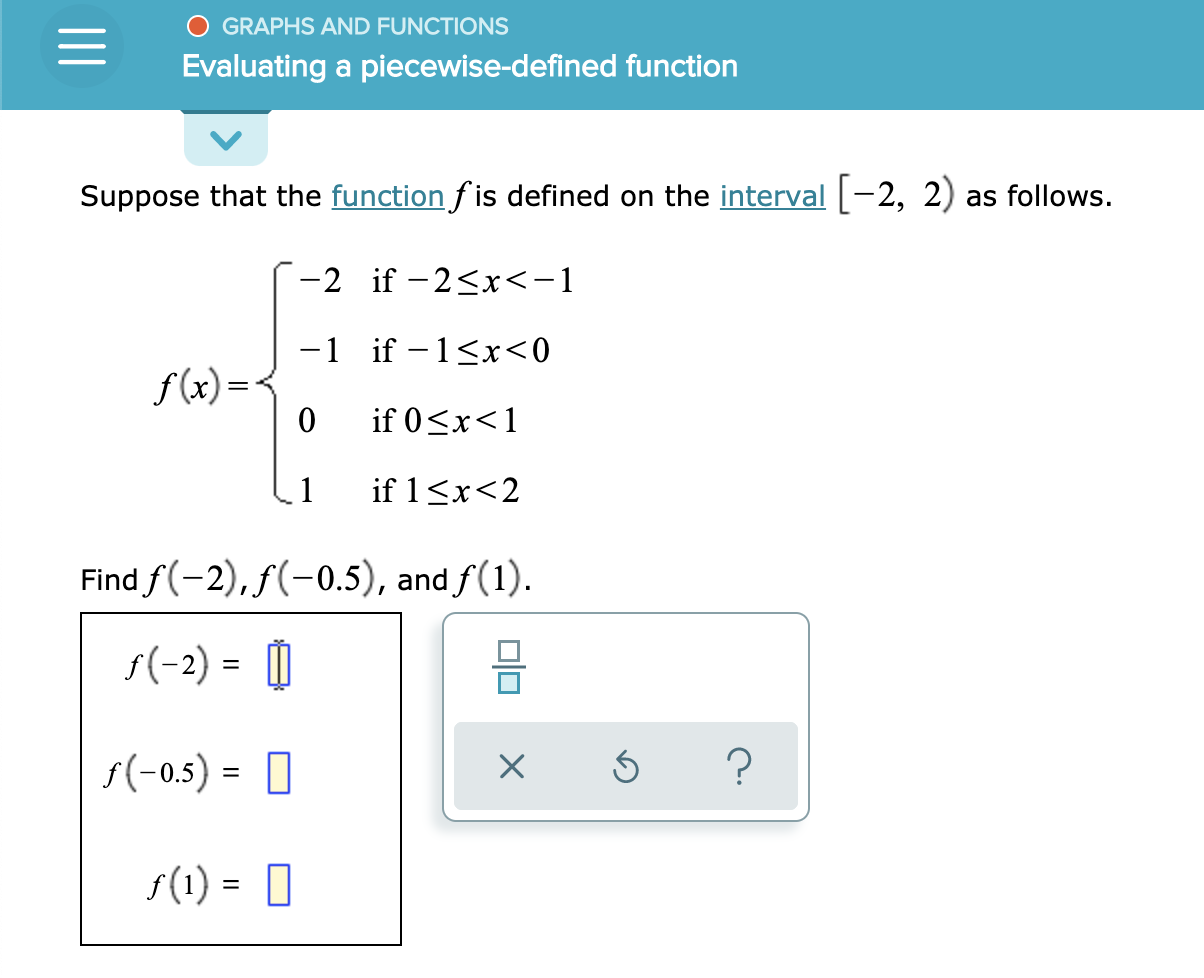
A closed circle indicates that the point is included in the interval An open circle indicates that the point is not included in the interval Intervals: To denote the edges of the loops, we are using the same notation as for the intervals of the solutions of the inequalities, remember? As you move each slider, constants and coefficients in the functions are changed, and thus the graphs of each function move to satisfy the new parameters. The following GeoGebra lab features several rational functions whose domains are defined by sliders. Hopefully you enjoyed that.Lesson Objective: This interactive lesson to help students understand of piecewise-defined functions.ĭefinition: A piecewise function is a function that consists of two or more standard functions defined on different domains. 10 Parabola, 142 Partial Riemann sums, 340 Piecewise continuous functions, 64 Piecewise-defined function, and the TI-83 graphing calculator. Type of function notation, it becomes a lot clearer why function notation is useful even. We have just constructed a piece by piece definition The value of our function? Well you see, the value of Solution We graph the line y x+3, except we leave a hole at the point ()3, 6, since 3 is deleted from the subdomain of the top rule. And x starts off with -1 less than x, because you have an openĬircle right over here and that's good because X equals -1 is defined up here, all the way to x is wdfw hunting pamphlet 2022 (Section 1.5: Piecewise-Defined Functions Limits and Continuity in Calculus) 1.5.5 Example 3 (Graphing a Piecewise-Defined Function with a Removable Discontinuity) Graph f, if fx() x +3, x 3 7, x 3. Give you the same values so that the function maps, from one input to the same output. If you are in two of these intervals, the intervals should So it's very important that when you input - 5 in here, you know which 5 into the function, this thing would be filled in, and then the function wouldīe defined both places and that's not cool for a function, it wouldn't be a function anymore. Important that this isn't a -5 is less than or equal to. Here, that at x equals -5, for it to be defined only one place. Over that interval, theįunction is equal to, the function is a constant 6. The next interval isįrom -5 is less than x, which is less than or equal to -1. If it was less than orĮqual, then the function would have been defined at This says, -9 is less than x, not less than or equal. It's a little confusing because the value of the function is actually also the value of the lower bound on this Over this interval? Well we see, the value
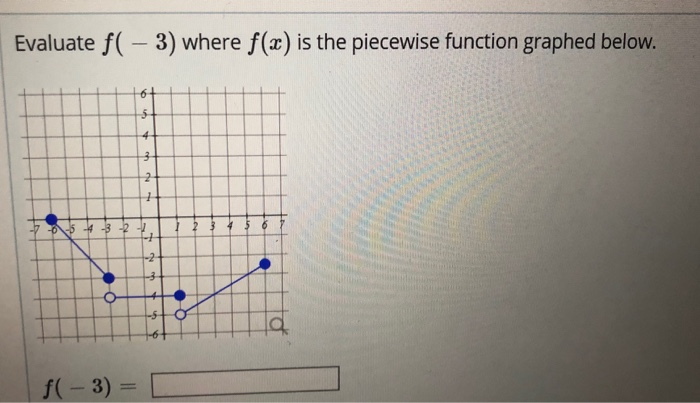
That's this interval, and what is the value of the function I could write that as -9 is less than x, less than or equal to -5. X being greater than -9 and all the way up to and including -5. Pan the graph (move it) by holding the Shift key and dragging the graph with the mouse. Use the following steps in Graph mode: 1) Enter the equation for the first interval. Sketching a piece-wise function means sketching the graphs of several functions with applied domains. Is from, not including -9, and I have this open circle here. A piecewise function is a function built from pieces of different. So let me give myself some space for the three different intervals. Then, let's see, our functionį(x) is going to be equal to, there's three different intervals. Over here is the x-axis and this is the y=f(x) axis.

Let's think about how we would write this using our function notation. In this interval for x, and then it jumps back downįor this interval for x.
#Piecewise defined function calculator free#
This graph, you can see that the function is constant over this interval, 4x. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with step-by-step explanations, just like a math tutor. View them as a piecewise, or these types of function definitions they might be called a But what we're now going to explore is functions that areĭefined piece by piece over different intervals By now we're used to seeing functions defined like h(y)=y^2 or f(x)= to the square root of x.


 0 kommentar(er)
0 kommentar(er)
